Welcome to this website for our collaborative project aimed at advancing the state-of-the-art in solution-verification, grid-adaptation and uncertainty quantification for chaotic turbulent flow problems. The project is funded by the Department of Energy and the National Nuclear Security Administration under the third installment of the Predictive Science Academic Alliance Program (PSAAP-III).

The name of this website -- "Turbulenza" -- is a version of the word "turbolenza" used by Leonardo Da Vinci to describe water flows more than 500 years ago. This project tries to emulate Da Vinci's polymath approach to science, by blending together rather deep mathematics, turbulence physics, advanced computer science, and a pragmatic engineering perspective.
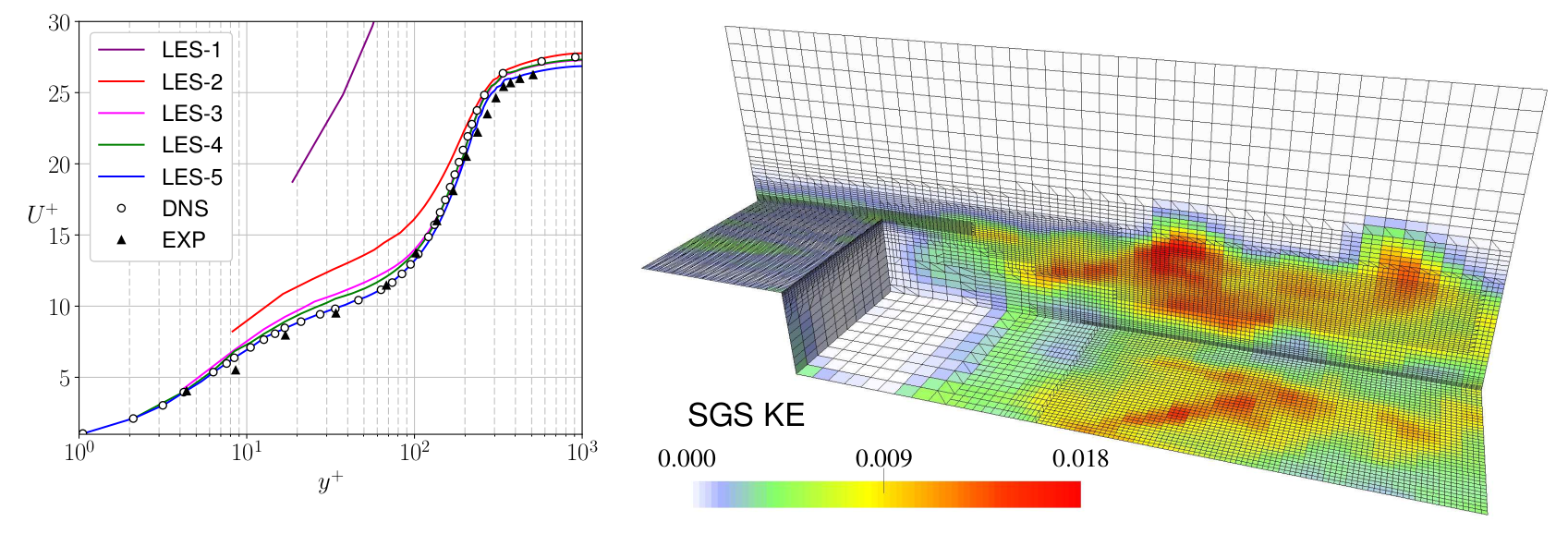
Turbulence is a chaotic phenomenon with broadband spectral dynamics for which there exists a range of different modeling approaches. Higher-fidelity modeling approaches produce solutions that retain the chaotic nature of turbulence, whereas lower-fidelity approaches produce non-chaotic dynamics. In general, the distinction comes down to whether the model directly resolves some of the turbulent dynamics (as in DNS or LES, or hybrid LES/RANS) or none of them (as in RANS). This project is focused on those turbulence-resolving simulation approaches that produce chaotic dynamics; most notably, large eddy simulation (LES).
The lack of credible yet affordable methods for Verification, Validation and Uncertainty Quantification (VVUQ) of chaotic turbulence-resolving simulations is a barrier to using such simulations to make critical decisions. The overall objective of this project is to produce research developments that overcome this barrier. The basic objective is to develop a mathematical foundation for VVUQ of models that exhibit chaotic dynamics. More specifically, this is broken down in the following sub-objectives: